1. Prove that for every prime
p,pn
does not divide
((p−1)∗n)!
.
2. Define a nice number as a rational number, with numerator and denominator positive and not exceeding some number.
N(x,y,n)
indicates the number of nice numbers, in
[0,n],a/b,a<=xandb<=y
, What is the formula for N?.
3. B.Stat question [Research problem conceived by me AFAIK]. Consider a prime number p. Consider all numbers having it as a factor. Repeatedly sum the digits of those numbers until you get a number less than or equal to p. In this sequence, will you ever get a p?2. How many numbers less than `n!` are divisible by all prime numbers less than `n`? What is the number for `1000`? Please show the work-out.
4. Prove that `2nCn` is always divisible by `2^{2}`, except when n is a power of 2.
5. Prove that `2^{n+1}C2^{n}` is divisible by 2, but not by 4, for all positive integral values of `n`.
6. Prove that, if `p` is a prime, then for any non-negative number `a`, `(a^p = a) mod p`.
7. Choose integer dimensioned rectangles (both width and height), so that, width `<= 2n` and height `<= 2n`. What is the probability that the resulting rectangle's areas is less than `n^{2}`.
a. If you were to bet on whether the resulting rectangles area will be less than `n^{2}` or not, what would you bet on?
8. Consider the quadratic equation `ax^2 + bx + c = 0`, with integer (not necessarily positive) co-efficients `a`, `b` and `c`, such that all of them are less than or equal to 100, in absolute value. How many numbers from 1 to 100 are roots of such an equation with some `a`, `b` and `c` combination?
9. Find the number for nice numbers (question 3), when numerator can exceed `x` and denominator can exceed `y`, but they should be reducible to something where they do not exceed `x` and `y`, respectively. If a formula is not possible, give an explanation why?
10. How many 4 digit numbers are there such that, the numbers are divisible by the sum of their digits?
11. How many 4 digit numbers are there such that, the numbers are divisible by the factorial of the sum of their digits?
12. How many 4 digit numbers are there such that, the minimal positive difference between their digits is 1. "minimal" means, if the number is `abcd`, then taking any combination like, `a + b + c - d` or `a - b - c + d` that results in a positive number, can one get 1? (Use only plus and minus).
13. How many 4 digit numbers are there such that, the product of the digits is not a perfect square, and not a perfect cube?
14. What is the minimum length of a string of digits, that contains all possible permutations of numbers 1 to 9?
15. Prove that such a string in 14, will be not be more than `9 * 9!` in length.
16. The distance between `2` permutations of numbers `1` to `n`, is defined as the least number of position flips, to make one permutation same as the other. For example, `123` is at a distance of `2` to `231`, because it can be got by first flipping `1` and `2` in `123`, getting `213`, then again flipping `1` and `3`, getting `231`
a. What is the minimum distance between two distinct permutations from `1` to `n`.
b. What is the maximum distance between two distinct permutations from `1` to `n`.
c. What is the sum of all pairwise distances of all permutations of `n` elements, from `1` to `n`. (Distance between `p_{a}` and `p_{b}` is counted only once, not twice).
17. In a `2m` page book, some sheets are missing. In how many ways, some `n` sheets that may be missing from the `2m` page book. (A sheet has `2` pages, no cover for the book).
18. `10000! = (100!)^{k} * p`, for some positive numbers k, p. Determine the maximum value for k.
19. Find the limit of `1/1! + 1/(1! + 2!) + 1/(1! +2! + 3!) + ...`, when the number of terms in denominator tends to infinity.
20. Prove that `1! + 2! + 3! + ... + n! < 2 * \sqrt{n} * ((n + e) / e)^n` for positive n.
21. Prove that `1! + 2! + 3! + ... + n! > (e + 1)/sqrt_{2 \pi} * (n / e)^n` for positive n.
22. Prove that `(6n + 4) C (3n + 2)` is always divisible by 3.
23. How many 10 digit numbers can be written as sum of 2 or more factorials?
24. Consider a quadrilateral to be a pythagorean, if all its sides are integers, and diagonal measures are also integers. Find all pythagorean quadrilaterals with dimensions (`<= N`).
25. Prove that `1 * 3 * 5 * 7 * .... * (4n - 1) < 2^{2n - 1} * (2n - 1)! * \sqrt{4n - 1}`. Try doing it without induction.
26. Prove that `(4n -1)! < 4^{2n-1} * ((2n -1)!)^{2} * \sqrt{4n - 1}`. No induction please.
27. Prove that there are infinitely many values of `n` for which `2nCn` is not divisible by a given odd prime number `p`.
28. Prove that `2nCn` is not divisible by a given prime number `p, iff all base `p` digits of `n` are less than `n/2`.
29. Prove that if `p` is a prime, `((p -1)! = (p - 1)) mod (p(p-1)/2)`.
30. Prove that if `p > 2` is a prime, `((p+1)^{p} = 1) mod p^{2}`.
31. Prove that if `p > 2` is a prime, `((p+1)^{p} = (p^{2} + 1)) mod p^{3}`.
32. Prove that if `p > 2` is a prime, `((p -1)! = -(p-2)! = 2(p-3)! = -6(p-4)!) mod p`.
33. Prove that if `p > 2` is a prime, `((p -1)! = (-1)^{j-1}*(p-j)!(j-1)!) mod p`.
34. Prove that if `p > 2` is a prime, `((p-2)! = 1) mod p`.
35. Prove that if `p > 2` is a prime, `((((p -1)/2)!)^{2} = (-1)^{((p+1)/2)}) mod p`.
36. The minimum length string, containing all permutation of `1, 2` and `3`, consists of 10 digits. Is it true or false?
a. In general, is it possible to achieve lower bound in question 15? Why? Why not?
37. How many 2 digit numbers are present such that, those have at most 2 factors.
38. How many 3 digit numbers are present such that, they can be written as sum of 2 squares.
39. Prove that only every 3rd number in fibonacci sequence is divisible by 2, only every 4th is divisible by 3, and every 5th by 5, and every sixth number is divisible by 8. What are the numbers for the lucas sequence? Prove them.
40. Prove that the number of prime numbers in first n fibonacci numbers, is never greater than the number of primes in the first n natural numbers.
41. Prove that, if an nth fibonacci number is a prime, then n is a prime. But the converse may not be true.
42. Prove that, if a fibonacci number is a square, there exist two other numbers such that, it is part of a pythagorean triple, along with those 2 numbers.
43. Prove that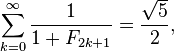
44. Prove that none of the lucas numbers are divisible by 5. Lucas series is given by Ln = ((1+sqrt(5))/2)^n + ((1-sqrt(5))/2)^n.
45. Prove also that, none of the lucas numbers are divisible by 13.
46. Prove that, if a sequence involves summing last two numbers to get the current number, it can't have all terms not divisible by 2.
47. Prove the same for 3. Prove the same for 4 also.
2. Define a nice number as a rational number, with numerator and denominator positive and not exceeding some number.
3. B.Stat question [Research problem conceived by me AFAIK]. Consider a prime number p. Consider all numbers having it as a factor. Repeatedly sum the digits of those numbers until you get a number less than or equal to p. In this sequence, will you ever get a p?2. How many numbers less than `n!` are divisible by all prime numbers less than `n`? What is the number for `1000`? Please show the work-out.
4. Prove that `2nCn` is always divisible by `2^{2}`, except when n is a power of 2.
5. Prove that `2^{n+1}C2^{n}` is divisible by 2, but not by 4, for all positive integral values of `n`.
6. Prove that, if `p` is a prime, then for any non-negative number `a`, `(a^p = a) mod p`.
7. Choose integer dimensioned rectangles (both width and height), so that, width `<= 2n` and height `<= 2n`. What is the probability that the resulting rectangle's areas is less than `n^{2}`.
a. If you were to bet on whether the resulting rectangles area will be less than `n^{2}` or not, what would you bet on?
8. Consider the quadratic equation `ax^2 + bx + c = 0`, with integer (not necessarily positive) co-efficients `a`, `b` and `c`, such that all of them are less than or equal to 100, in absolute value. How many numbers from 1 to 100 are roots of such an equation with some `a`, `b` and `c` combination?
9. Find the number for nice numbers (question 3), when numerator can exceed `x` and denominator can exceed `y`, but they should be reducible to something where they do not exceed `x` and `y`, respectively. If a formula is not possible, give an explanation why?
10. How many 4 digit numbers are there such that, the numbers are divisible by the sum of their digits?
11. How many 4 digit numbers are there such that, the numbers are divisible by the factorial of the sum of their digits?
12. How many 4 digit numbers are there such that, the minimal positive difference between their digits is 1. "minimal" means, if the number is `abcd`, then taking any combination like, `a + b + c - d` or `a - b - c + d` that results in a positive number, can one get 1? (Use only plus and minus).
13. How many 4 digit numbers are there such that, the product of the digits is not a perfect square, and not a perfect cube?
14. What is the minimum length of a string of digits, that contains all possible permutations of numbers 1 to 9?
15. Prove that such a string in 14, will be not be more than `9 * 9!` in length.
16. The distance between `2` permutations of numbers `1` to `n`, is defined as the least number of position flips, to make one permutation same as the other. For example, `123` is at a distance of `2` to `231`, because it can be got by first flipping `1` and `2` in `123`, getting `213`, then again flipping `1` and `3`, getting `231`
a. What is the minimum distance between two distinct permutations from `1` to `n`.
b. What is the maximum distance between two distinct permutations from `1` to `n`.
c. What is the sum of all pairwise distances of all permutations of `n` elements, from `1` to `n`. (Distance between `p_{a}` and `p_{b}` is counted only once, not twice).
17. In a `2m` page book, some sheets are missing. In how many ways, some `n` sheets that may be missing from the `2m` page book. (A sheet has `2` pages, no cover for the book).
18. `10000! = (100!)^{k} * p`, for some positive numbers k, p. Determine the maximum value for k.
19. Find the limit of `1/1! + 1/(1! + 2!) + 1/(1! +2! + 3!) + ...`, when the number of terms in denominator tends to infinity.
20. Prove that `1! + 2! + 3! + ... + n! < 2 * \sqrt{n} * ((n + e) / e)^n` for positive n.
21. Prove that `1! + 2! + 3! + ... + n! > (e + 1)/sqrt_{2 \pi} * (n / e)^n` for positive n.
22. Prove that `(6n + 4) C (3n + 2)` is always divisible by 3.
23. How many 10 digit numbers can be written as sum of 2 or more factorials?
24. Consider a quadrilateral to be a pythagorean, if all its sides are integers, and diagonal measures are also integers. Find all pythagorean quadrilaterals with dimensions (`<= N`).
25. Prove that `1 * 3 * 5 * 7 * .... * (4n - 1) < 2^{2n - 1} * (2n - 1)! * \sqrt{4n - 1}`. Try doing it without induction.
26. Prove that `(4n -1)! < 4^{2n-1} * ((2n -1)!)^{2} * \sqrt{4n - 1}`. No induction please.
27. Prove that there are infinitely many values of `n` for which `2nCn` is not divisible by a given odd prime number `p`.
28. Prove that `2nCn` is not divisible by a given prime number `p, iff all base `p` digits of `n` are less than `n/2`.
29. Prove that if `p` is a prime, `((p -1)! = (p - 1)) mod (p(p-1)/2)`.
30. Prove that if `p > 2` is a prime, `((p+1)^{p} = 1) mod p^{2}`.
31. Prove that if `p > 2` is a prime, `((p+1)^{p} = (p^{2} + 1)) mod p^{3}`.
32. Prove that if `p > 2` is a prime, `((p -1)! = -(p-2)! = 2(p-3)! = -6(p-4)!) mod p`.
33. Prove that if `p > 2` is a prime, `((p -1)! = (-1)^{j-1}*(p-j)!(j-1)!) mod p`.
34. Prove that if `p > 2` is a prime, `((p-2)! = 1) mod p`.
35. Prove that if `p > 2` is a prime, `((((p -1)/2)!)^{2} = (-1)^{((p+1)/2)}) mod p`.
36. The minimum length string, containing all permutation of `1, 2` and `3`, consists of 10 digits. Is it true or false?
a. In general, is it possible to achieve lower bound in question 15? Why? Why not?
37. How many 2 digit numbers are present such that, those have at most 2 factors.
38. How many 3 digit numbers are present such that, they can be written as sum of 2 squares.
39. Prove that only every 3rd number in fibonacci sequence is divisible by 2, only every 4th is divisible by 3, and every 5th by 5, and every sixth number is divisible by 8. What are the numbers for the lucas sequence? Prove them.
40. Prove that the number of prime numbers in first n fibonacci numbers, is never greater than the number of primes in the first n natural numbers.
41. Prove that, if an nth fibonacci number is a prime, then n is a prime. But the converse may not be true.
42. Prove that, if a fibonacci number is a square, there exist two other numbers such that, it is part of a pythagorean triple, along with those 2 numbers.
43. Prove that
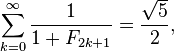
44. Prove that none of the lucas numbers are divisible by 5. Lucas series is given by Ln = ((1+sqrt(5))/2)^n + ((1-sqrt(5))/2)^n.
45. Prove also that, none of the lucas numbers are divisible by 13.
46. Prove that, if a sequence involves summing last two numbers to get the current number, it can't have all terms not divisible by 2.
47. Prove the same for 3. Prove the same for 4 also.
48. Prove that if such a sequence also does not have 5 as a factor, prove the cycle 2134 (modulo 5) occurs in such a sequence (Similar to the lucas sequence).
49. What is/are the sub-sequences in case of 13? Can there be other sequences (with different cycles), or, only similar to lucas possible there?
49. What is/are the sub-sequences in case of 13? Can there be other sequences (with different cycles), or, only similar to lucas possible there?
No comments:
Post a Comment